Automated Market Making on Kalshi

How Cognitive Financial Agents optimize Stochastic Control Problems

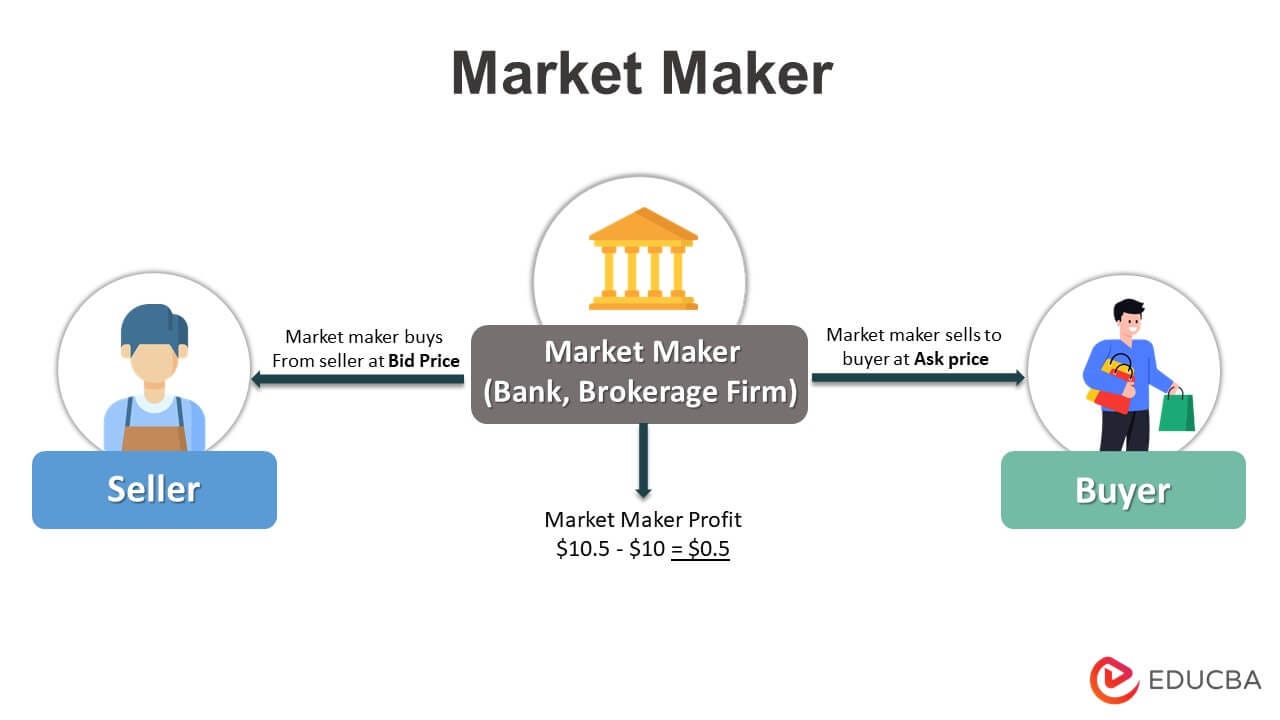
I recently noted this interesting project about automated market-making on the alternative investment platform Kalshi after seeing this discussion on YC’s Hackernews. In the rare case that you don’t know, Kalshi is a regulated event futures exchange where users can trade on the outcome of real-world events. Market making in general is a fundamental function in modern financial markets, providing liquidity by continuously quoting both buy and sell prices. And Kalshi is not that different in that regard. This helps to reduce price volatility and ensure smoother trading by allowing investors to buy or sell assets without significant delays. Modern market making, especially in high-frequency trading, was significantly influenced by the 2008 Avellaneda-Stoikov model, developed by Marco Avellaneda and Sasha Stoikov. Their model provides a mathematical framework for optimizing market-making strategies and balancing profit potential with inventory risk. Market makers generate profit through price arbitrage of the bid-ask spread (the price difference between buy and sell orders)

In this post, I will discuss Stochastic Control Problems and ideas to improve market-making with Cognitive Financial Agents.

Market Makers (MM) on Kalshi

It is in Kalshi’s best interest that there is enough liquidity on the platform and that trades are executed quickly. Therefore, Kalshi introduced the MM program which is aimed at credible partners to support Kalshi at enhancing market liquidity and ensuring fair trading practices. While everybody can apply, to qualify, applicants have to pass an evaluation process assessing their financial stability, relevant experience, and business reputation. Benefits of becoming a Kalshi market maker include financial incentives, reduced fees, adjusted position limits, and enhanced platform access.

source

The market maker has to answer three fundamental questions.

1. What does the market think the asset is worth?

2. What do I think the asset is worth?

3. What is my existing inventory of this asset?

This leads to these two fundamental risks a market maker faces:

Inventory risk: The potential for significant losses due to adverse price movements while holding inventory. This risk becomes particularly acute during periods of high volatility or when market makers accumulate large positions due to one-sided order flow. The cost of hedging these positions must be carefully weighed against potential profits. Therefore in any model, we should penalize large inventory positions, encouraging the agent to rebalance to neutral holdings over time.

and

Execution risk: The uncertainty surrounding whether quoted prices will result in executed trades. This includes both the risk of missed trading opportunities when spreads are too wide and the risk of adverse selection when spreads are too tight.

Market makers, as shown in High-Frequency Trading in a Limit Order Book, must constantly balance these competing risks while maintaining competitive quotes.

For a slightly simplified model, the market maker's risk management actions are based on optimizing these variables:

• Reservation price: A dynamically adjusted mid-price based on the state of inventory.

• Optimal spread: The bid-ask spread (depends on risk appetite and market conditions).

How can this be done?

Stochastic Control Problems (SCP)

Stochastic control problems are optimization problems where decisions are made sequentially under uncertainty. The system evolves over time based on both the decision-maker’s actions and stochastic (random) influences, often modeled as a Markov process. Since the goal is typically to minimize a cost function or maximize a reward function over a given time horizon it lends itself to supporting the challenges of the market maker. You might already see where I am going with this.

SCP’s have the following core components:

1. State Space: Represents current market conditions—order flow, spread, mid-price movements, and liquidity imbalances.

2. Control: The set of actions available to the decision-maker. Usually bid-ask quotes and inventory adjustments

3. Dynamics: The transition law, is often governed by a stochastic differential equation or a Markov decision process (MDP). The next state depends on the current state, action, and a random noise term.

4. Cost/Reward Function: Defines the objective, usually an expectation over future discounted rewards or costs. Typically minimizes inventory risk while maximizing expected revenues from the bid-ask spread, often formulated as an expected reward over a finite or infinite horizon

5. Policy: A strategy mapping states to actions.

Automated Market Making as a Stochastic Control Problem

What makes AMM an interesting proposition for Cognitive Financial Agents, is that automation needs to operate in a volatile, adversarial environment where optimal pricing and inventory management require continuous decision-making under uncertainty. We already know that market makers must balance profitability and inventory risk, as holding too much of one asset exposes them to adverse price movements. The underlying dynamics follow a stochastic process, where execution probabilities depend on the posted prices relative to order flow distributions.