Evaluating Consciousness and Reasoning in Abstract Strategic Games (I)

Random vs Reinforcement Learning vs Qwen Agents. Who would win the most?

Oct 20, 2024

Tic Tac Toe is a simple game.

Most of us know the rules of this game since we were children. Tic Tac Toe (from here on TTT) is an example of an abstract strategy game that is played on an NxN board. In its simplest and most common form, the board size is 3 x 3, but for this exercise, the larger boards are significantly more interesting.

source

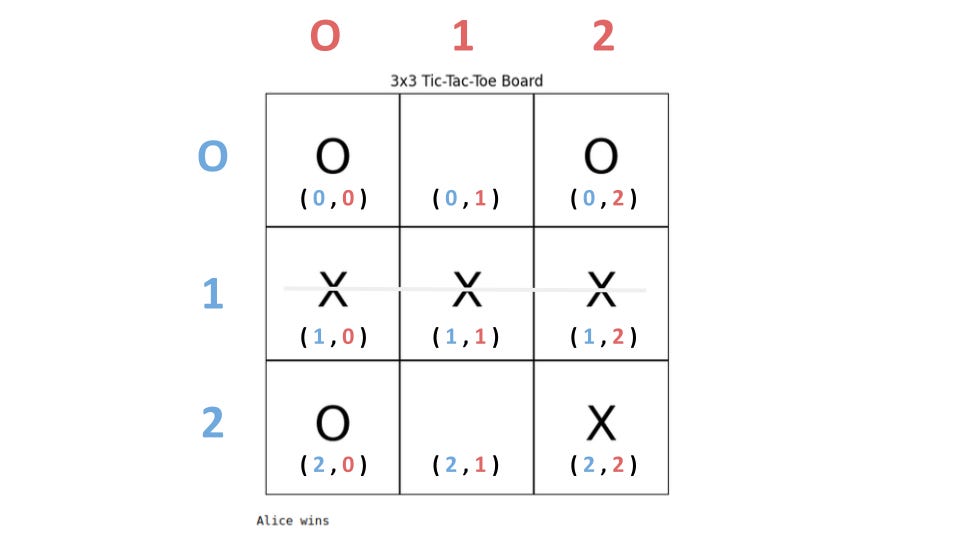
To play the game, each player chooses a symbol, usually either X or O, and the winner is the one who first completes a vertical, horizontal, or diagonal row. Above is an example of a 3x3 board and the 7-step winning moves that explain the concept.

Historically, TTT-type games date back thousands of years. Its origins can be traced to ancient Egypt, where a game called Seega was played as early as 1300 BC. The Romans later played a variation called "Terni Lapilli" (three pebbles) where players placed their pieces on a grid of lines, but instead of writing symbols, they used tokens.

In the 19th and 20th centuries, the game became a common pastime in many Western countries, often played on paper or blackboards as it is one of the simplest strategy games that can end in a win, loss, or draw, making it popular as an introduction to strategic thinking.

This simplicity made TTT a prime candidate for computer implementations with the earliest examples of a computerized version (OXO) developed in 1952 by Alexander S. Douglas as part of his Ph.D. dissertation on human-computer interaction. Similar to my series on Game Theory (i, ii, iii), this post will have part I (setup and first findings) and part 2 (tournament and implementations of advanced concepts.

For this exercise, I will be implementing a game of TTT with 3 player archetypes.

A Random player — A player that just selects a move from all possible states.
A Reinforcement Learning player — Who has been trained on more than 100,000 games.
A Qwen2.5-based Cognitive ReAct agent that “reasons” each move.

It will be interesting to see which contender will come out on top and maybe answer the question of whether a Cognitive ReAct agent understands the nature of the game.

As usual, the code will be made available for paying subscribers first.

What I think makes TTT an interesting follow-up to the series of game theoretical games I did prior is that it looks simple and is quite easy to implement. In my mind, that makes it an easy peer-reviewable project.

Generalizing the game

Let’s dive into a couple of statistics about the game.

The total possible states of a game have an upper limit of 3^(n^2). The “3” represents the three possible states for each cell on the board ( “empty”, “X”,” O”) while “n” represents the size of the board.

Here is a simple example of what that would mean.

As you can see, the complexity increases exponentially so for a 3x3 board we have 19,684 possible configurations while for a 5x5 we already have 3^25 ≈ 8.47 × 10^11. I.e., 847 Billion. Important to note is that this includes symmetries, invalid games, and states where the game is already won. Therefore, the actual number of unique game states is much lower. 765 for a 3x3 board and an estimated 10^8 states for a 5x5 board.

Within the context of this exercise, I plan to play games up to 64x64.

One thing that makes smaller boards uninteresting to play for humans is the first-move advantage. In 3 x 3 boards this is statistically 58.5%. Drivers of this advantage are that the first mover can dictate the initial flow of the game and force a response.

What I observed though is that the larger the boards get, the more this first-mover advantage decreases.

This could be attributed to:

Harder winning condition: If it remains "n-in-a-row" where n is board size, larger boards make it harder to achieve a win.
Strategic depth: Larger boards offer more possibilities, reducing the impact of the initial move.
Defensive play: With more space, the second player has more options to block and counter.
Game length: Longer games on larger boards allow more opportunities for both players to make meaningful moves.
Computational complexity: As the board size increases, perfect play becomes harder to achieve, potentially reducing the first player's theoretical advantage.

Therefore, I have encoded the game to allow play on a dynamic set of dimensions helping me to study these effects in more detail. We have learned at my posts about Graph Reasoning that the encoding of the problem is half the work.

Encoding the Game

Let’s start with encoding the game by defining the board first. Most people are more familiar with the 3x3 board, therefore I will stick with this for now. For the board, I decided to use a tuple structure that is similar to the dimensions within a matrix instead of starting to count from 1-9.

That makes sometimes validating the results a bit harder, but it feels more natural and it matches the matrix logic used in tree-traversing and generally machine learning. We instantiate the empty board with this one-liner.

self.board = np.zeros((_ROWS,_COLS))

What are the tasks that the game needs to be able to facilitate?

Initialize the board → Board Object
Creates an empty matrix of a “board” representation, assigns two players, and an ending condition..

Provide all available positions → Array of Tuples

Loops i,j over the game board and appends all unset positions.

def availablePositions(self):
        positions = []
        for i in range(_ROWS):
            for j in range(_COLS):
                if self.board[i, j] == 0:
                    positions.append((i, j))  # needs to be tuple
        return positions

Update the Board after the move of a player

Operates on the board to set the selected move of a player and activates the next active player.

def updateState(self, position):
        
        self.board[position] = self.playerSymbol
        
        # activate next player
        self.playerSymbol = -1 if self.playerSymbol == 1 else 1

Reset the board after the game is over → None

Straightforward. Clears all variables and activates the default “first player”.

def reset(self):
        self.board = np.zeros((_ROWS, _COLS))
        self.boardHash = None
        self.isEnd = False
        self.playerSymbol = 1

Visualize the board → Matplotlib
Monitoring this exercise is half the fun as it makes you feel like Matthew Broderick in the movie War Games. I implemented two functions one with a simple print and the other using Matplotlib.
Give reward → Player
Once a game has been won, lost, or drawn the game loop rewards the players for their performance. The RL player can use this to optimize their policy during training. Fundamentally this is quite simple. And since the game is structured quite simply, it is not necessary to refine this further at this stage.
Run to game loop → Gamestate
This is two big loops. One that runs over the number of games we want to play. This is especially important when training the RL Player since here the game will optimize its policy of the player giving rewards for good performance.
The key functionality here is to loop until the isEnd condition is not met, provide the current state of the board and all available positions, trigger the players to make their move (“act”) and reset the board once the game is over.

Encoding the players

To begin this exercise, I will, as introduced prior, implement three different players that all are derived from one player archetype as a Python base class since the only difference between them is how they implement their “act” method and how they need the reward for good performance. I did not implement a human player.

Does the player always start with the same move?

I noticed that the RLPlayer occasionally does that. Hence, I ensured that the first move was always random. I.e., if no game has been played and you are an active player.

if len(self.game_state)==0 and symbol==1:
   action=random.choice(positions)

Let’s start with the act method of the Random player since it is the easiest. The role of the random player in the context of this exercise is to be like the Joker in Batman. A voice of chaos that aims to challenge established patterns.

action=random.choice(positions)

The RL Player is naturally more complicated than this and selects its move by maximizing the move with the potentially highest reward. Again, the agent starts with a brute-force approach to loop over all possible positions and aims to find the one that minimizes its loss function.

if action is None:

    value_max = float('-inf') #Ensure that you will always find one

    for p in positions:  # Loop over all possible positions
        next_board = current_board.copy()
        next_board[p] = symbol  
        next_boardHash = self.getHash(next_board)

        _val=self.states_value.get(next_boardHash)
        value = 0 if _val is None else _val
                  
        if value >= value_max:
           value_max = value  # Find the one that maximizes value
           action = p

Once a move has been found, this position is returned as the next value. In 3x3 board their training evolves around hashing the board structure with a max length of 9 possible positions. Once a full game is over the RLPlayer receives its reward.

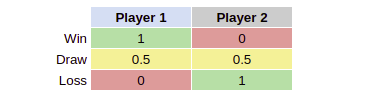
The table is from the perspective of Player 1.

This brought up two questions.

Would a player miss a winning move?
Would a player miss an obvious losing move?

The answer in both cases is yes. Therefore, I also have included a “cheat” mode where that can be activated at will to allow the agent to block a game-losing move therefore potentially forcing a draw and a win condition that if the agent deterministically detects if there is a way to win, to choose that option. The motivation is to have the agent behave like a real human being since most human players would block a winning move of the other player and clearly select the winning move.

The Agent Player

Probably the most interesting one of the three. Since it’s the only one that is based on “new tech”. The agent uses the remote HFApiEngine and utilizes Qwen2.5-72B-Instruct in the same way I had introduced them before ( agent, prompt).

The key components of this agent are

Initialize as a ReactJsonAgent from the Transformer’s library with the default system prompt.

Provide a custom task to the agent. I tried to be as close to the semantics of the system prompt as possible.

task=f"""You are a smart assistant that can play Tic Tac Toe really well.  I will give you the current state of the game board, possible positions, and your player id. Select from positions just one position and return it.  
You MUST return a valid Json object that returns exactly one move and one thought. 
     1. the move must be a position on the board [x,y]
     2. the thought must explain why you decided on this move. 
Remember your MUST win the game. Play aggressively to win. Block only to avoid losing. Do not try to escape special characters. 
Based on your success you have received this accumulated $REWARD {self.reward}. $positions {positions}, $board {current_board}, $your player id {symbol}."""

Parsing the agent’s response.
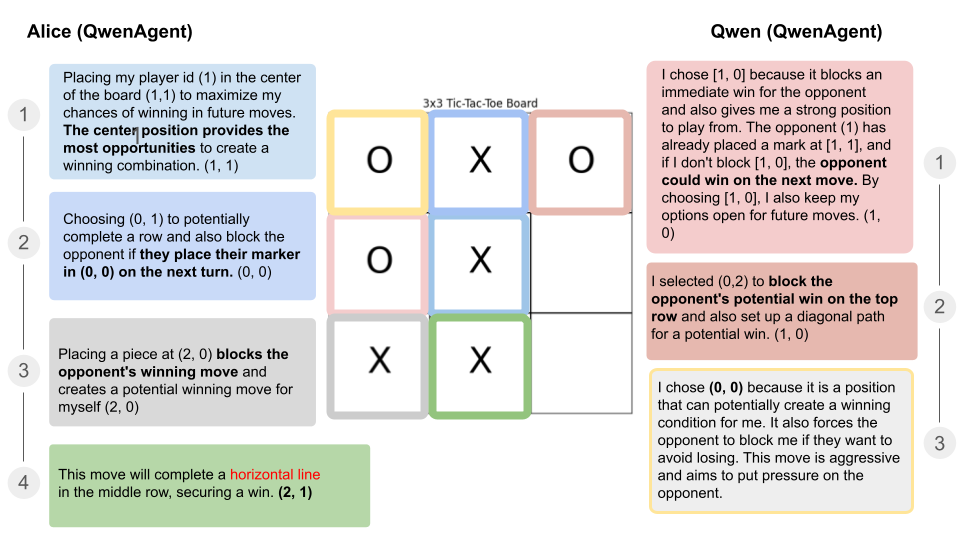
One gotcha I ran into quite early was a tuple is not valid JSON. Therefore, the agent returns the coordinates in square brackets. I also wanted to understand the reasoning of the agent. Specifically, since I am using the ReAct pattern. Therefore, I tasked the agent to return that as well. And to be frank, I found the response really interesting already.

Preliminary Results

If we consider two ReAct agents playing against each other. What will happen?

Observation 1: The games were executed in a stable way. There were no skipped moves because the output was not readable. All provided moves were valid. And logically made sense without reading too much into it. I suppose the benefit of selecting that specific game was that it in 100% of all cases results in a termination.

Observation 2: Analyzing the thought patterns will be a task on its own. In the sample game, one of the agents mentioned that there was a winning move (red) in the middle row that was interesting and correct, even though the line was not horizontal but vertical. This could be due to an encoding error though.

I suppose the next step now is to define the tournament parameters more clearly especially focusing on how to evaluate conditional success conditions given draws.

In closing

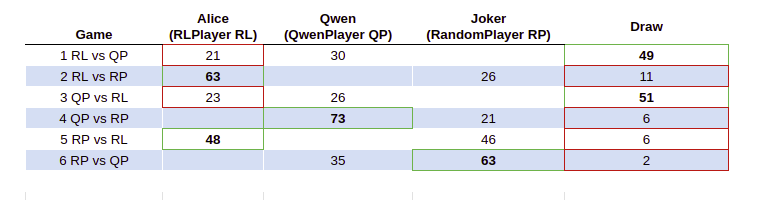
When running the initial naive tournament with 100 games on a 3x3 board we observe that QwenPlayer comes out slightly on top, while RLPlayer Alice beats the Joker handsomely. Interestingly, the reverse game is more even. This can be explained through the first-mover advantage being almost 2/3 games won when playing first. Hence, I hold the opinion that playing on 3x3 is actually quite boring for this type of analysis.

As preparation for part 2 of this exercise, I aim to fine-tune the players and the correct board size.

Contender 1: The Random player
Contender 2: The default RLPlayer
Contender 3: The RL-trained player with “cheat” mode enabled, i.e., proactive performing game-losing blocks and game-winning moves
Contender 4: The RL-trained player trained with optimizing MinMax algorithm.
Contender 5: A Cognitive ReAct Agent with all the information in the prompt
Contender 6: A Cognitive ReAct Agent seeded with a game-winning strategy
Contender 7: A Cognitive ReAct Agent playing Negamax as a function.
Contender 8: A Cognitive ReAct Agent performing graph reasoning.

I have not decided yet if I want to compare different LLMs since I enjoy working with Qwen and think it makes more sense to optimize one LLM.

This post is getting long and I will wrap it up here.

Thank you for reading this far. Please share it would help me a lot to keep this going.